[模組] 三軸重力加速計 Accelerometer (GY-61 ADXL335)
模組介紹
三軸重力加速計是一種重力感測器,也稱為加速規或加速計。三軸指的是 X, Y, Z 軸,重力加速度就是我們高中理化曾學過的地心引力 (g)。由於這個重力加速度是地球的天然資源 (就像磁力線的指南針),所以當我們身體傾斜或翻轉時,透過地心引力的影響讓身體內部機構可感受到其傾斜或翻轉。於是,將此概念應用到科技工業上,像電玩的體感遊戲 (Wii, Kinect...)、飛行器、懸臂旋轉、震動感測...等都使用到相關元件,本文針對三軸重力加速計的晶片做測試研究,希望能獲得更多的應用靈感。首先,找一顆晶片試試吧!Arduino 開發套件常見的三軸加速計,使用的是 ADI ADXL335/345 晶片,因此我買了一個來測試玩玩看,並用 NXP LPC1114 晶片來設計系統。
三軸重力加速計晶片是 MEMS 設計工藝,能將這種感測技術設計到小晶片裡面,不得不佩服這群工程人員。由於地表的重力加速度有方向性,晶片又根據該重力為基準來測量三軸的變化,所以晶片與三軸的方向座標必須先定義好,如下面圖一所示,晶片面朝上為 Z軸。以圖一為例,晶片放置水平,量測到的重力數值為 X 軸 0g, Y 軸 0g, Z軸 1g。然後,該晶片內部再將這三軸的物理量轉換成電壓值輸出。實驗中,我手上拿到的是 ADXL335,它是輸出三軸的電壓值,所以設計系統時需要選用具有 ADC 功能的 MCU ,才能將這三個電壓值轉換回重力值。此外,ADI 還開發另一顆 ADXL345 晶片,與 ADXL335 晶片有些不一樣的地方,前者內部已有包含 ADC 功能,能將重力值直接轉換成數位值,並使用 I2C / SPI 介面和外部通訊,提供使用者不同的選擇。
圖一:晶片的三軸方向座標
規格分析
三軸重力加速計晶片在使用前先要找到 0g 的電壓值,這也是校正歸零的步驟。雖然每顆晶片出廠前都經過測試,但是每顆晶片之間的物理特性還是存在一點點差距,這種差距還算是合理範圍,只是我們必須用校正的方式將它拉到同一標準內,消除這種誤差。底下圖二所示為晶片的規格,當 0g 的時候,電壓輸出是 1.5V,所以我將晶片放成水平後,X/Y軸讀到的電壓約 1.58V 左右,也就是這兩軸差不多為 0g (規格的測試環境是 Vs = 3V,我的環境是 Vs = 3.3V)。接著,看規格裡的靈敏度,從歸零點起算每增加 1g 電壓值增加 300mV。因此,晶片放成水平後,Z軸讀到的電壓約 1.9 V左右,也就是差不多 1g,符合規格的定義。當翻轉晶片時,座標有方向性,所以重力值有正負之分,電壓值低於 1.5V 就是圖一的軸座標往下了。
圖二:ADXL335晶片的規格,包括 0g 的標準電壓與靈敏度
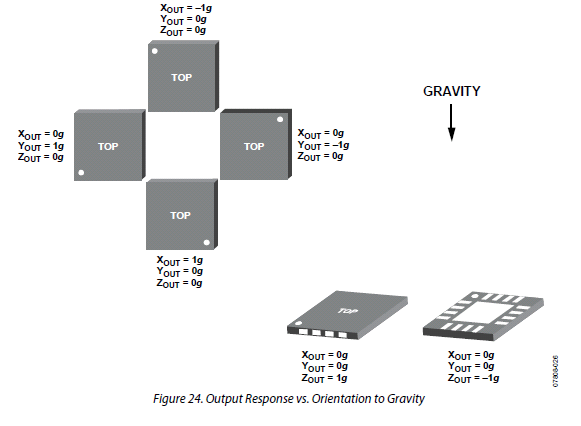
底下圖三是電壓值轉重力的程式代碼,我使用的是 NXP LPC1114 具有 10-bit ADC 的控制晶片。首先,先找到晶片的規零數值,如下面的 490 就是我這顆晶片的 0g (約 1.579V)。以此為基準點,每 330mV 增加 1g,轉換的公式如圖三內所示。另外,驗證水平與直立的重力值,如下面圖四所示。圖四的右下角,當針對單一X軸作旋轉時,晶片水平面朝上,則 Z 軸會量測到 1g;若晶片水平面朝下,則 Z 軸會量測到 -1g。左半邊的圖則是測試晶片面垂直於地面的情況 (相當於 Z 軸與地平面平行),則 X 或 Y 軸分別會量測到 1g。
圖三:電壓值轉重力的程式代碼
圖四:晶片針對某一軸旋轉後,每軸所讀取的重力值
實現展示
底下的影片是我將 ADXL335 模組做旋轉的測試,觀察每一軸的重力值之變化,同時比對該重力值與上面的圖四左半圖結果是否一致。影片中,我先將模組直立與地面盡量保持垂直,並順時針旋轉,觀察 X, Y 軸的重力值,LCD 顯示的數值單位是 mg (重力加速度)。最後,再將模組平放,觀察 Z 軸的重力值。基本上,實驗結果重力值的正負號結果如同圖四的標示,但絕對數值則有些誤差。
上面的實驗都是測試水平與垂直的重力變化,屬於兩軸的變化。如果要了解三度空間旋轉的角度,需要先把高中物理和三角函數的觀念從記憶中喚回來。第一步,我們將 Y 軸固定在水平面,這樣 Y 軸的重力為 0g。接下來,以 Y 軸為中心旋轉 X, Z 軸,如圖五所示。假設 Z 軸往 X 軸順時針旋轉了一個角度後,依據物理分量的觀念,重力加速度可看成具有 gx 和 gz 的分量,而這兩個分量分別可從晶片量測而得到。再根據三角函數的定義,我們可以計算出旋轉的角度,如下所示。
上述的推導是以 Y 軸為中心,旋轉其他兩軸。以此類推,固定 X 軸為水平後,我們也可以推導出 Z 軸往 Y 軸旋轉的角度。於是整合推導的觀念後,三軸的空間便能從每一軸的分量計算出該軸對其它兩軸的旋轉角度了,定義為(θ,φ)。最後,我們把三度空間想像成一個球體,從計算出的旋轉角度(θ,φ)可以知道目前晶片面對哪一方位,請參考高中數學的球體方程式。
實驗時,將晶片水平放置,沿著 X 軸前後移動,可以發現 gx 重力值變化明顯,而 gz 重力值沒有變化 (些微的變動)。如果沿著 Y 軸前後移動,則換成 gy 重力值會出現明顯變化,同樣 gz 重力值沒有變化,也就是水平的移動不會對垂直的 Z 軸產生影響。
影片:旋轉模組,觀察各軸的重力值
上面的實驗都是測試水平與垂直的重力變化,屬於兩軸的變化。如果要了解三度空間旋轉的角度,需要先把高中物理和三角函數的觀念從記憶中喚回來。第一步,我們將 Y 軸固定在水平面,這樣 Y 軸的重力為 0g。接下來,以 Y 軸為中心旋轉 X, Z 軸,如圖五所示。假設 Z 軸往 X 軸順時針旋轉了一個角度後,依據物理分量的觀念,重力加速度可看成具有 gx 和 gz 的分量,而這兩個分量分別可從晶片量測而得到。再根據三角函數的定義,我們可以計算出旋轉的角度,如下所示。
上述的推導是以 Y 軸為中心,旋轉其他兩軸。以此類推,固定 X 軸為水平後,我們也可以推導出 Z 軸往 Y 軸旋轉的角度。於是整合推導的觀念後,三軸的空間便能從每一軸的分量計算出該軸對其它兩軸的旋轉角度了,定義為(θ,φ)。最後,我們把三度空間想像成一個球體,從計算出的旋轉角度(θ,φ)可以知道目前晶片面對哪一方位,請參考高中數學的球體方程式。
圖五:旋轉角度的計算原理
實驗時,將晶片水平放置,沿著 X 軸前後移動,可以發現 gx 重力值變化明顯,而 gz 重力值沒有變化 (些微的變動)。如果沿著 Y 軸前後移動,則換成 gy 重力值會出現明顯變化,同樣 gz 重力值沒有變化,也就是水平的移動不會對垂直的 Z 軸產生影響。









留言